
Since x = 1 does not satisfy the original inequality, the region is not part of the solution. Since x = 0 does satisfy the original inequality, the region is part of the solution. Since x = –1 does not satisfy the original inequality, the region is not part of the solution. Select points from the regions created (see Figure 5). Mark the boundary points using solid circles, as shown in Figure 4, since the original inequality includes equality. Represent the solution in graphic form and in solution set form. Since x = –3 satisfies the original inequality, the region x 3 is part of the solution. See whether the test points satisfy the original inequality. Select points from the different regions created (see Figure 2). Here, the boundary points are open circles because the original inequality does not include equality (see Figure 1). If a test point satisfies the original inequality, then the region that contains that test point is part of the solution. Replace these “test points” in the original inequality. Select points from each of the regions created by the boundary points. Make the boundary points solid circles if the original inequality includes equality otherwise, make the boundary points open circles. The real solutions to the equation become boundary points for the solution to the inequality. Solve the inequality as though it were an equation. To solve a quadratic inequality, follow these steps: Quiz: Binomial Coefficients and the Binomial Theorem.Binomial Coefficients and the Binomial Theorem.Quiz: Definition and Examples of Sequences.Quiz: Exponential and Logarithmic Equations.Systems of Inequalities Solved Graphically.Quiz: Systems of Equations Solved Graphically.

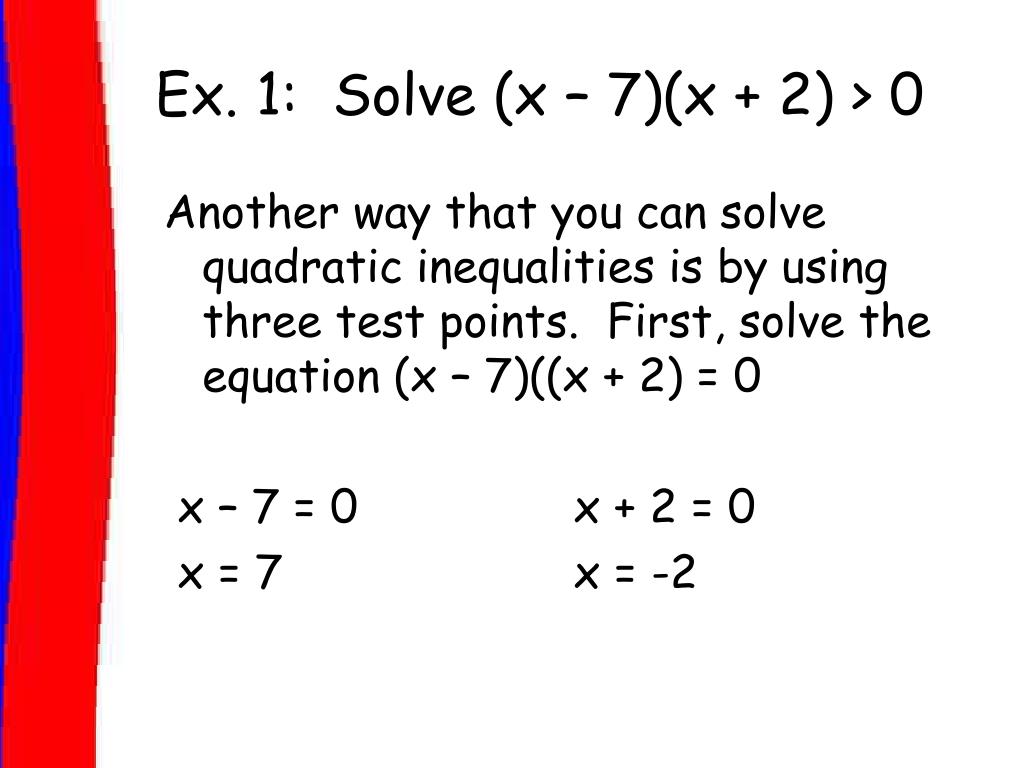
Linear Equations: Solutions Using Matrices with Three Variables.Linear Equations: Solutions Using Elimination with Three Variables.Quiz: Linear Equations: Solutions Using Elimination with Three Variables.Quiz: Linear Inequalities: Solutions Using Graphing with Two Variables.Linear Inequalities: Solutions Using Graphing with Two Variables.

Quiz: Linear Equations: Solutions Using Determinants with Two Variables.Linear Equations: Solutions Using Determinants with Two Variables.Quiz: Linear Equations: Solutions Using Matrices with Two Variables.Linear Equations: Solutions Using Matrices with Two Variables.Quiz: Linear Equations: Solutions Using Elimination with Two Variables.Linear Equations: Solutions Using Elimination with Two Variables.Quiz: Linear Equations: Solutions Using Substitution with Two Variables.Linear Equations: Solutions Using Substitution with Two Variables.Quiz: Linear Equations: Solutions Using Graphing with Two Variables.Linear Equations: Solutions Using Graphing with Two Variables.Quiz: Slopes of Parallel and Perpendicular Lines.Slopes of Parallel and Perpendicular Lines.


 0 kommentar(er)
0 kommentar(er)
